I’d like to introduce a joint work with Junzhe Zhang and Elias Bareinboim, titled Sequential Causal Imitation Learning with Unobserved Confounders, which we presented at NeurIPS 2021. While the paper is a collaboration, the opinions and description here are my own.
This post is divided into 5 sections. The first is geared towards a general audience, and explains the problem’s basics. The second section shows how we encode this problem and how an answer would look, with the goal of being comprehensible to someone familiar with causal diagrams. The third section introduces imitation in sequential contexts, and the fourth section gives a taste of our contribution, geared towards a more technical audience. Finally, the post concludes with a brief discussion of our method’s limitations.
What Problem are we Solving?
Let’s use the example of building a self-driving car. Some carmakers are trying to develop these vehicles by gathering data on how humans drive, and then training a computer to behave the same way. In other words, with enough examples of people stopping at red lights, it is hoped that the machines will begin associating red lights with stopping, and behave correctly.
This is called imitation learning, because the machine (imitator) is being trained to copy a human (demonstrator). This problem has a strong theoretical foundation when both the demonstrator and the imitator see the same context (i.e. identical sensors), because with infinite data and exploration, the imitator will observe the environment and the demonstrator’s actions in every possible situation, and can then repeat the expert’s actions when acting itself!
Things fall apart once the demonstrator and imitator have different views of the world, whether through different vantage points (a person sitting in back of a car doesn’t have a full view of the road) or different sensors (a deaf person won’t react to sounds). For example, current self-driving systems are based on cameras/lidar, and generally don’t include microphones. This means that while most human drivers (demonstrators) can hear and react to sounds, the self-driving car (imitator) cannot. What would happen if this deaf machine were trained to copy the behavior of a human driver who stopped their car after hearing screeching tires and people yelling? Since it might not see anything around it, it could conclude that a good driver should sometimes slam on the brakes for no reason!
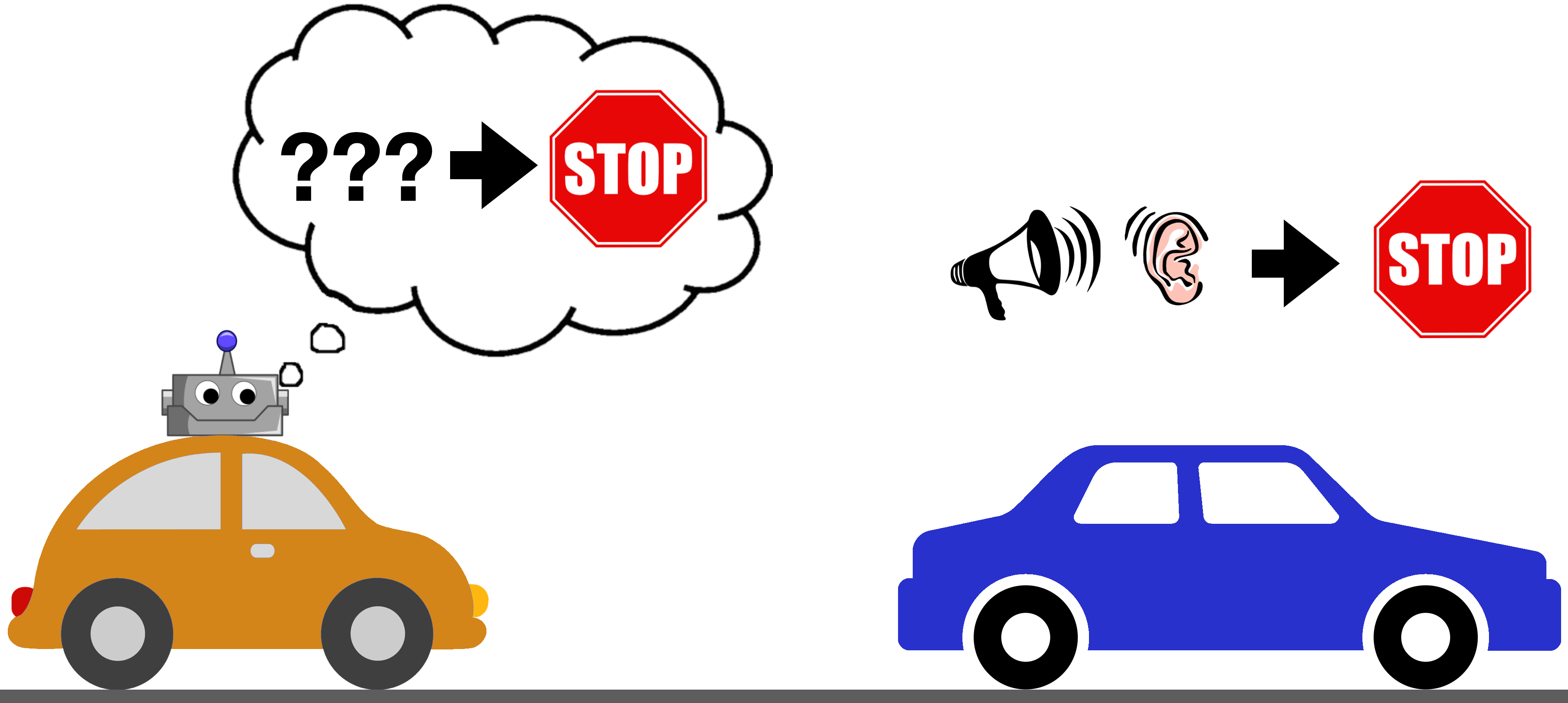
Is there a way to avoid this type of situation? Can we have guarantees that the imitator will learn the right thing despite a mismatch in sensors and observations?
You might notice that when reasoning about the problem above, I told a story of how things were related, and what caused what. The person can hear, and sounds can reflect road conditions, which in turn can influence how the driver should behave. In order to approach the problem mathematically, we will encode this understanding of the world’s structure in a way that can be processed algorithmically.
When given a detailed description on how things are causally related, our method can then determine whether it is possible for the imitator to compensate for missing sensors. If such compensation is possible, the imitator can still have overall performance identical to that of the demonstrator, despite having a different view of the environment.
Causal Imitation
In our work, description of the environment is achieved using causal diagrams [1]. These acyclic graphs encode how variables in the system are related[1]. To demonstrate, consider a continuation of the self-driving car example, where we are given a toy causal structure.
In this toy example, the car’s surroundings are represented by events to the front, back, and side of the car, and are drawn in the diagram below using F,B and S nodes. Whether or not someone is a good driver (reward,
In the ideal case, after observing the human’s driving for a while, we would then give the imitator (
Not all is lost here - we can add side and back cameras to the self-driving car, giving the imitator direct access to B and S, shown below. We proved in [3] that this is sufficient to compensate for the lack of a microphone in this toy example, allowing for the imitator to learn a policy for action
On the other hand, if we can’t install side cameras on the car, we end up with the situation below (S and H are both unobserved by the imitator), making the imitator incapable of taking into account events to the side of the vehicle. We can tell this is generally impossible by imagining how information can flow through the causal graph. Suppose that we flip a coin at S - if it is heads, there is a car crash to the side, if tails, there is nothing. There is the sound of a crash (H) if and only if there is a crash. Finally, a good driver slams on the brakes if and only if there is a crash. Without side cameras, the self-driving car can’t know when there was a crash, and therefore can’t know when to stop, leading to worse performance than the human driver who can hear the crash.
We call this situation “Not Imitable”, because no matter what the self-driving car does, it doesn’t have the ability to behave indistinguishably from the demonstrator with respect to the reward
Sequential Causal Imitation
The single-action setting was handled in our previous work [3]. This section will describe the basics of the sequential setting, which allows us to tackle situations where the agent must make multiple actions per episode.
In the simplest case, consider the causal diagrams below. Just like before, we draw the expert’s actions in blue, and the imitator’s actions in orage. Despite the expert making use of a latent variable W for its actions, the imitator can pretend to know W by choosing actions
The above example was relatively straightforward, since
Suppose that we have the graph to the left below, with variables determined in the order U,
In other words, depending on the causal diagram, the imitator might sometimes be able to recognize which of its actions are relevant towards imitation, and when it can compensate for previously-made errors!
Sequential
Before finishing this post, I will briefly describe our main contribution: a necessary and sufficient graphical condition for determining imitability based on the causal diagram. Like in the previous examples, the imitator uses a specific set of observed variables at each action. If these sets of observed variables satisfy the criterion, a policy trained on them will give identical performance as the demonstrator. If there are no sets of variables which can satisfy the criterion, then there is at least one distribution consistent with the causal diagram for which no imitating policy exists.
Using the same diagram as the previous example, we can choose the empty set
With these graphs, we can state the criterion:
Sets
associated with actions satisfy the Sequential -Backdoor criterion if for each action , and at least one of the following holds in :
(1)with all edges from to its children removed, or
(2)is not an ancestor of
To demonstrate, let’s check if
With the criterion satisfied, we can train a policy
Finally, the full paper also describes a polynomial-time algorithm to find sets
Limitations & Discussion
The work described here is a purely theoretical and mathematical treatment of imitation. It requires a causal diagram as input, and returns the sets of variables which lead to performance identical to an expert. The causal diagram is often not available in practical situations, and current methods of learning them from observational data lead to equivalence classes [5]. This work would need to be extended to work in such contexts, and therefore it might take some time before the utility of these results can be fully realized.
Instead, this paper can be seen as a single step in a larger push towards awareness of latent variables and confounding in imitation and reinforcement learning. Knowledge of the the conditions under which current methods are guaranteed to work, and an understanding of the limitations of current approaches to causal inference for imitation learning might lead to a deeper understanding of the tradeoffs and assumptions we make when teaching machines to learn from others.
Our graphs are related to Causal Influence Diagrams [2], with the difference that our decision nodes are decisions made by the demonstrator, and therefore act as observations from the imitator’s perspective. ↩︎
The value of Y is determined by
. Given that the mechanisms of are identical when expert and imitator are active, if both imitator and expert have identical , then they will result in identical distributions over . ↩︎
References
- Pearl, J. (2000). Causality: Models, Reasoning and Inference.
- Dawid, A. P. (2002). Influence Diagrams for Causal Modelling and Inference. International Statistical Review / Revue Internationale de Statistique, 70(2), 161–189. www.jstor.org
- Zhang, J., Kumor, D., & Bareinboim, E. (2020). Causal imitation learning with unobserved confounders. Advances in Neural Information Processing Systems, 33.
- Koller, D., & Friedman, N. (2009). Probabilistic Graphical Models: Principles and Techniques. MIT press.
- Glymour, C., Zhang, K., & Spirtes, P. (2019). Review of Causal Discovery Methods Based on Graphical Models. Frontiers in Genetics, 10, 524. https://doi.org/10.3389/fgene.2019.00524